Fluiddruck
Die bei einem nach Kapitel Grenzflächen sich in Ruhe befindlichen Fluid wirkende Kraft $$F$$ pro Flächeneinheit $$A$$ wird als Druck $$p$$ mit der Einheit [Pa] bzw. [N/m²] bezeichnet. Gebräuchlich ist auch die Einheit 1 [bar] = $$10^5$$ [Pa].
Im Grenzfall $$\lim_{A\rightarrow 0}$$ erhält man den Druck in einem Fluidpunkt.
\begin{equation}
% \begin{aligned}
p = {\frac{F}{A}
= \lim_{dA\rightarrow 0} \frac{dF}{dA}}
% \end{aligned}
\end{equation}
Richtungseinfluss auf den Druck
Dieser Druck $$p$$ kann durch äußere Kräfte (Pressung durch einen Kolben) oder innere Kräfte (Gewichts-, Trägheitskräfte) hervorgerufen werden. An einem herausgeschnittenen Prisma innerhalb einer Flüssigkeit soll ermittelt werden, ob der vorliegende Druck richtungsabhängig und somit als Vektor zu betrachten ist oder ob er unabhängig von der Flächenrichtung und somit als Skalar betrachtet werden kann.

Angreifende Druckkräfte am Flüssigkeitsprisma
Die Vorgabe des Gleichgewichtszustands einer ruhenden Flüssigkeit bedingt, dass nach Abb. Angreifende Druckkräfte am Flüssigkeitsprisma die drei resultierenden Kräfte $$F_1$$, $$F_2$$ und $$F_3$$ senkrecht auf den Flächen
$$A_1$$, $$A_2$$ und $$A_3$$ stehen. Die Kräfte $$F_i$$ wirken in den einzelnen Schwerpunkten $$S_i$$ und werden mit den gemittelten Drücken $$\overline{p}_i$$ ermittelt. Aus dem Gleichgewichtszustand lässt sich jeweils die resultierende Kraft in x- bzw. y-Richtung bestimmen.
\begin{equation}
\sum{F_{ix}} = {0 = F_1 – F_3 \cdot sin \alpha}
\end{equation}
Mit
\begin{equation*}
\overline{p}_1=\frac{F_1}{a \cdot l}, ~~\overline{p}_2~=~\frac{F_2}{b \cdot l},~~ \overline{p}_3~=~\frac{F_3}{c \cdot l}~~ \mathrm{und}~~ sin \alpha = \frac{a}{c}
\end{equation*}
ergibt sich für das Kräftegleichgewicht in x-Richtung:
\begin{align}
\overline{p}_1 \cdot a \cdot l ~&=~ \overline{p}_3 \cdot c \cdot l \cdot sin \alpha
\nonumber \\
%\overline{p}_1 \cdot c \cdot sin \alpha &= \overline{p}_3 \cdot c \cdot sin \alpha \\
\overline{p}_1 &= \overline{p}_3
\end{align}
In analoger Weise ergibt sich das Kräftegleichgewicht in y-Richtung
\begin{equation*}
\sum{F_{iy}} = 0 = F_G + F_3 \cdot cos \alpha – F_2 ~~\mathrm{mit}~~ \sum{F_G} = \rho \cdot g \cdot \frac{a \cdot b}{2} \cdot l
\end{equation*}
zu
\begin{align}
\rho \cdot g \cdot \frac{a \cdot b}{2} \cdot l + \overline{p}_3 \cdot c \cdot l \cdot cos \alpha &= \overline{p}_2 \cdot b \cdot l
\nonumber \\
\overline{p}_2 &= \overline{p}_3 + \rho \cdot g \cdot \frac{a}{2}~~.
\end{align}
Im Fall eines infinitesimal kleinen Prismas mit $$\lim\limits_{a \rightarrow 0}$$ durch Parallelverschiebung der Seite $$c$$ in den Punkt $$P$$ erhält man
\begin{equation}
\overline{p}_1 ~= ~ \overline{p}_2~=~\overline{p}_3
\end{equation}
Somit ist der Druck $$p$$ in irgendeinem Punkt $$P$$ des sich im Gleichgewicht befindlichen Mediums (flüssig oder gasförmig) nur von den Koordinaten abhängig und somit eine skalare Größe.
Druckfortpflanzung
Wird durch eine äußere Kraft, z.B. durch einen Hydraulikkolben, Druck auf ein Medium in einem geschlossenen Volumen ausgeübt, so herrscht dieser Druck unabhängig von der Form des Volumens gleichmäßig an allen Wänden. Die resultierende Kraft wirkt hierbei senkrecht auf jedes Flächenelement (Abb. Druckfortpflanzung innerhalb eines geschlossenen Volumens). Diesem Druck können weitere Kräfte wie die Gewichtskraft bzw. Fliehkräfte überlagert werden.
Druckfortpflanzung innerhalb eines geschlossenen Volumens
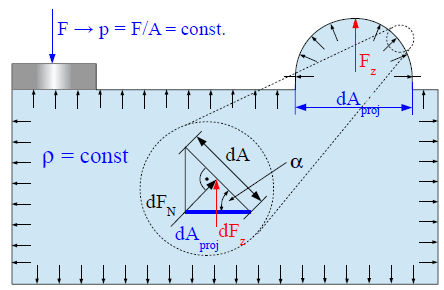
Druckkraft auf gekrümmte Flächen
Stehen beliebig geformte Behälter bzw. Deckel unter Druck, so stellt sich die Frage, welche resultierende Kraft auf die jeweiligen Flächen wirkt. In Abb. Druckfortpflanzung innerhalb eines geschlossenen Volumensgehen wir davon aus, dass die wirkenden Gewichtskräfte klein gegenüber den durch Pressung erzeugten Druckkräften sind. Somit wirkt mit $$dF_N ~= ~ p \cdot dA$$ auf die halbkugelförmige Fläche des Deckels die resultierende Kraft
\begin{align}
dF_Z &= dF_N \cdot cos \alpha
= p \cdot dA \cdot cos \alpha ~~.
\end{align}
Unter Verwendung von $$dA \cdot cos \alpha ~=~ dA_{proj}$$ folgt hieraus für die Gesamtkraft
\begin{align}
dF_Z = p \cdot dA_{proj} \nonumber \\
F_Z = \int\limits_A {dF_z} ~= ~ p \cdot \int\limits_A{dA_{proj}} \nonumber \\
= p \cdot A_{proj}
\end{align}
Sichern Sie sich jetzt das komplette Wissen als PDF (100% Gratis!)

Kostenloses PDF-Skript zur Strömungsmechanik
Sparen Sie wertvolle Zeit mit allen wichtigen Informationen zur: Strömungsmechanik, Hydrostatik, Aerostatik und vielem mehr…
