Kraft eines Freistrahls auf eine schräge ebene Wand in Ruhe
Trifft ein inkompressibler stationärer Freistrahl ($$\dot{V}_1=konstant$$) unter dem Winkel $$\alpha$$ schräg auf eine feststehende ebene Wand, so entstehen entlang der Wand zwei ablaufende Strahlenden mit den Abflüssen $$\dot{V}_2=v_2 \cdot A_2$$ und $$\dot{V}_3= v_3 \cdot A_3$$, wobei gilt $$\dot{V}_1= v \cdot A = \dot{V}_2 + \dot{V}_3{.}$$
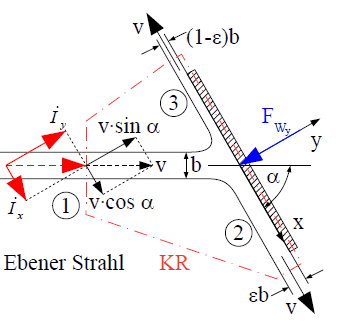
Kraft auf eine schräge ebene Platte
Bestimmt werden soll die Normalkomponente $$F_{W_y}$$ der Wandkraft.
Da die drei Fluidstrahlen eine freie Oberfläche haben, ist der Druck in den Querschnitten 1-3 gleich dem Umgebungsdruck und die entsprechenden Druckkräfte entfallen. Das lokale Koordinatensystem ist so gewählt, dass bei reibungsfreier Strömung die Kräfte in x-Richtung gleich Null sind.
Für den Freistrahl folgt nach Bernoulli $$v=v_1=v_2=v_3$$.
Aus der Kontinuitätsgleichung folgt
$$\dot{V}_1=\dot{V}_2+\dot{V}_3$$ und mit $$\dot{V_1}_x = \dot{V}_1\cdot cos \alpha$$
im xy-Koordinatensystem:
\begin{equation}
\begin{aligned}
\dot{V_1}_x + \dot{V}_2 -\dot{V}_3 &= 0 \nonumber \\
\dot{V}_1\cdot cos \alpha + \dot{V}_2 -(\dot{V}_1 -\dot{V}_2) &= 0 \nonumber \\
\dot{V}_2&= \dot{V}_1 \cdot \frac{1-cos\alpha}{2} \nonumber \\
\dot{V}_2&= \dot{V}_1 \cdot \epsilon \nonumber \\
\dot{V}_3&= \dot{V}_1 \cdot (1-\epsilon)
\end{aligned}
\end{equation}
Somit ergibt sich die Strahlaufteilung bei einer unter dem Winkel von 90° senkrecht zum Freistrahl stehenden Platte zu $$\epsilon=1/2$$, d.h. der Strahl wird in zwei gleich große Volumenströme geteilt.
Es ergibt sich die in y-Richtung senkrecht auf den Freistrahl wirkende Kraft $$F_{W_y}$$:
\begin{equation}
\begin{aligned}
\sum{{F_y}_i} &= 0 \nonumber \\
\dot{m} \cdot v_y – F_{W_y} &= \nonumber \\
(\rho \cdot v\cdot A_1) \cdot v_y – F_{W_y} &= \nonumber \\
(\rho \cdot v \cdot A_1) \cdot v \cdot sin\alpha – F_{W_y} &= \nonumber \\
F_{W_y} &= \rho \cdot v² \cdot A_1 \cdot sin\alpha
\label{eqn:F_y_ebene_Platte}
\end{aligned}
\end{equation}
Bei einem Winkel der ebenen Platte von 90° zum Freistrahl ergibt sich die senkrecht zur Wand auf den Freistrahl wirkende Kraft zu
$$F_y = \rho \cdot v^2 \cdot A_1$$,
welche nach dem Prinzip actio=reactio die Reaktion der Wand auf die Aufprallkraft des Freistrahls darstellt.
Wird der Freistrahl als Ausflussstrahl mit dem Querschnitt $$A_1$$ mit der Ausflussgeschwindigkeit nach Torricelli ( $$v=\sqrt{2 \cdot g \cdot h}$$) angenommen, so folgt aus der Gleichung für die maximale Druckkraft (auf die ebene Platte unter 90°):
$$F_{W_y}= \rho \cdot A_1 \cdot (2 \cdot g \cdot h)$$
Kraft eines Freistrahls auf eine schräge ebene Wand in Bewegung
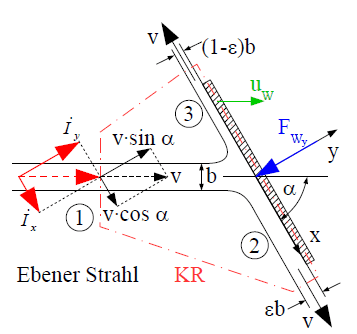
Kraft auf eine schräge ebene Platte in Bewegung
Die Kraft eines Freistrahls auf eine ebene Wand in Bewegung lässt sich analog zur Vorgehensweise in Kap. Kraft eines Freistrahls auf eine schräge ebene Wand in Ruhe ermitteln. Da sich die Wand selbst bewegt, ergibt sich die resultierende Geschwindigkeit $$v_{res}$$ durch Addition der Wandgeschwindigkeit zur Geschwindigkeit des Fluids
$$ \vec{v}_{res} = \vec{v} + \vec{u}_W{.}$$
Hierbei muss die Bewegungsrichtung der Wand beachtet und im Vorzeichen berücksichtigt werden.

Tabelle Relativgeschwindigkeit in Abhängigkeit der Bewegungsrichtung der Wand
Sichern Sie sich jetzt das komplette Wissen als PDF (100% Gratis!)

Kostenloses PDF-Skript zur Strömungsmechanik
Sparen Sie wertvolle Zeit mit allen wichtigen Informationen zur: Strömungsmechanik, Hydrostatik, Aerostatik und vielem mehr…
