Kraft auf eine am Boden gelagerte rechteckige Klappe

Kraft auf eine am Boden gelagerte rechteckige Klappe

 
Die folgende Berechnung ist nur gültig, wenn das Fluid bis zum obersten Punkt der Klappe reicht und die Kraft $$F_{Klappe}$$  senkrecht am obersten Punkt der Klappe angreift.

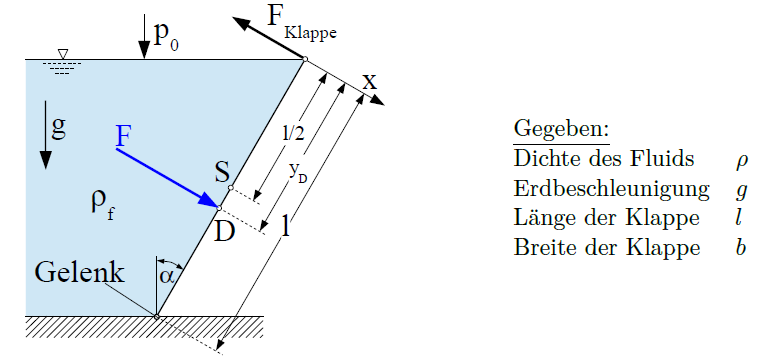
Kraft auf eine schräge am Boden gelagerte Klappe

Druckkraft $$F_{Fluid}$$ auf die Klappe:
\begin{equation}
\begin{aligned}
F_{Fluid} ~&=~ \rho \cdot g \cdot h_S \cdot A \\
~&=~ \rho \cdot g \cdot \frac{1}{2} \cdot l \cdot cos\, \alpha \cdot (b \cdot l ) \\
~&=~ \frac{1}{2} \cdot \rho \cdot g \cdot l² \cdot b \cdot cos\, \alpha
\end{aligned}
\end{equation}

Flächenschwerpunkt $$S$$ der Klappe:
\begin{equation}
y_S ~=~ \frac{1}{2} \cdot l
\end{equation}

Flächenträgheitsmoment $$I_S$$ im Flächenschwerpunkt $$S$$:
\begin{equation}
I_S ~=~ \frac{1}{12} \cdot l³ \cdot b
\end{equation}

Lage $$y_D$$ des Druckmittelpunktes $$D$$:
\begin{equation}
\begin{aligned}
e ~&=~ \frac{I_S}{A \cdot Z_S} \\
~&=~ \frac{l³ \cdot b}{12} \cdot \frac{1}{b \cdot l} \cdot \frac{1}{l/2} \\
~&=~ \frac{l}{6}
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
y_D ~&=~ y_S ~+~ e \\
~&=~ \frac{1}{2} \cdot l ~+~ \frac{1}{6} \cdot l \\
~&=~ \frac{2}{3} \cdot l
\end{aligned}
\end{equation}

Momentengleichgewicht um das Gelenk:
\begin{equation}
\begin{aligned}
F_{Klappe} \cdot l ~&=~ F_{Fluid} \cdot (l ~-~ y_D) \\
F_{Klappe} ~&=~ \frac{l ~-~ y_D}{l} \cdot F_{Fluid} \\
~&=~ \frac{l}{3} \cdot F_{Fluid}
\end{aligned}
\end{equation}

zurück zu Kraft auf eine runde Absperrklappe

weiter zu Fluidkraft auf eine gekrümmte Wand